天然氣場站工藝管道腐蝕速率的 FOA-SVM模型預測
來源:《管道保護》雜志 作者:王志月 張劍鋒 屠明剛 時間:2019-3-21 閱讀:
王志月 張劍鋒 屠明剛
中石油管道有限責任公司西氣東輸分公司
摘 要:針對天然氣場站工藝管道結構復雜、高壓力、流速快等特點,在應用多元統計分析算法的基礎上,采用果蠅優化算法(FOA)對支持向量機(SVM)管道內腐蝕預測模型進行優化訓練,建立FOA-SVM預測模型,具有建模結構簡單、非線性擬合好、參數少、易調節、易于理解和實現等特點,利用125個實測數據樣本對模型的預測結果進行檢驗,綜合方差和均差為1.397×10-3、 0.0374,相比灰色模型和BP神經網絡預測結果更貼近實際值,避免了BP神經網絡模型預測局部最優和灰色模型誤差大的缺點,為管道剩余使用壽命和剩余強度計算提供有力的數據支撐。
天然氣長輸管道是國家能源輸送的生命線和動脈,具有接受天然氣、給管道天然氣增壓、分輸天然氣、配氣、儲氣調峰、發送和接受清管器等功能,是天然氣輸送過程中的關鍵環節。由于天然氣集輸過程中伴隨CO2、 H2S、雜質等有害物質的腐蝕,以及流速對管道的沖刷腐蝕,管道腐蝕的隨機性、模糊性使得腐蝕因子與腐蝕速率之間的關系呈現著復雜的非線性關系,會造成集輸管線斷裂、爆炸及泄漏,破壞下游用戶的平穩供氣,帶來的危害不僅給國家造成很大的經濟損失,也威脅工作人員的生命安全。現今關于預測管道內腐蝕速率的算法較多[1-6],單一的模型已經不能滿足預測精度的需求,如陳永紅[5]等將灰色系統理論與馬爾科夫相結合,建立灰色馬爾科夫組合模型,得到了灰色無偏優化模型,使得預測數據得到了提升;胡松青[6]等建立的BP神經網絡模型對輸油管道內腐蝕速率預測進行預測,預測了硫含量、酸值、溫度、壓力、流速因素對管道內腐蝕規律的影響。本文中所述的FOA-SVM模型對天然氣場站工藝管道內腐蝕速率的預測與實測數據、灰色馬爾科夫組合模型、BP神經網絡模型進行對比分析,結果表明FOA-SVM模型預測值更為準確,避免了BP神經網絡模型預測局部最優和灰色模型誤差大的缺點,確定了預測管道內腐蝕速率新方法。
1 SVM基本理論
SVM是由統計學理論而來,主要針對小樣本數據進行學習、分類和預測的一種方法,“低維空間”上的點或線映射到“高維空間”,尋找一個平面將這些點或線分離,這種線形函數統稱為“超平面” [7,8]。通過松弛變量和核函數(Kernel)處理實現低維到高維的轉化,線性不可分轉化為可分,最后對轉化之后的樣本進行線性分析[9-12]。
假設樣本為(χ1 ,χ2 , ...χn .)∈Rn, (y1 ,y2 ,...yn .)∈R, χ∈RN 為輸入參數, y∈R為相應的輸出參數, n為樣本個數。 SVM的轉化過程就是建立一個非線性映射Φ ,將數據χ映射到高維特征空間F,回歸函數為[9]:

根據多元統計分析理論,可通過以下目標數極小化確定SVM回歸函數:
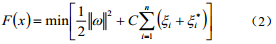
約束條件為:
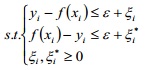
拉格朗日對偶性變量約束優化:
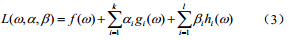
約束條件為:
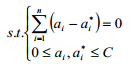
式(1)—(4)中:α i,α i—拉格朗日系數;
αi, β i—拉格朗日算子;
b—臨界值;
ω—權值矢量;
ξ ,ξ*—非負松弛變量;
С—懲罰變量;
ε—不敏感損失函數參 數;
Κ (χi,χj)—SVM的核函數。
核函數是計算兩個向量在隱式映射空間中的內積函數,將低維空間中向量通過變換得到高維空間量的向量內積值,文中選用高斯徑向基核函數,即:K(xi,xj)=exp(-g|xi-xj|2),g為核函數的參數寬度。
通過以上的理論推導可得到回歸函數為:
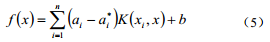
對于新的輸入參數x可通過該式計算得到相應的輸出值。
2 果蠅算法優化支持向量機
果蠅優化算法是一種基于果蠅覓食行為而推演出尋求全局群智能優化的新方法,屬于演化式計算的范疇,亦屬于人工智能的領域,可混合其他方法與管道內腐蝕技術一起使用,如模糊數學、經驗公式、灰色系統與神經網絡等。通過果蠅自身位置來估計周圍的味道濃度,隨后果蠅向味道濃度的極值方向飛去,重復迭代味道濃度求取目標函數的最優解[12-14]。
由于果蠅是在三維空間飛行,而原始的FOA算法是在二維空間搜尋全局極值,因此將可能導致無法搜尋到三維空間中的最佳值,因此本文采用三維空間搜尋,對FOA進行改進。
FOA對SVM優化的具體步驟,見圖 1所示。
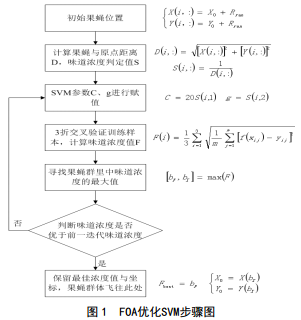
圖 1式中:Rγαn —隨機數;i=1,2,…m;yij—真實值;m—各個交叉驗證訓練子集的果蠅數目;f(χij)—交叉訓練的預測值;bF-F的最大值;bI-F最大值所處的位置。
因為SVM的優化參數是С和 g,所以 X 和 Y 均為m 行2列矩陣。采用迭代的方法對參數進行優化,同時判定味道濃度相比上一次迭代的味道濃度變化,如果優于上一步迭代則轉至步驟(7),否則繼續循環直至達到指定循環次數N時,循環終止。
3 FOA-SVM管道內腐蝕速率預測模型
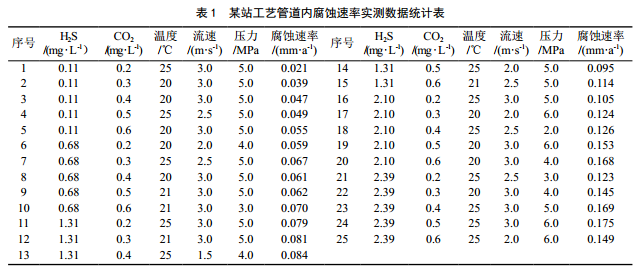
某站管道材質為20#鋼, 2003年10月建成投產,使用壓力為4~7 MPa,輸送介質為天然氣,影響管道內腐蝕速率主要參數為H2S、 CO2、溫度、流速、壓力,實測數據統計見表 1。將影響內腐蝕速率的參數作為輸入向量,內腐蝕速率作為輸出向量,建立FOA-SVM預測模型。選取某輸油站管道內腐蝕速率實測數據1~25組樣本作為訓練集,以某站實驗數據作為測試集,采用實測值與灰色馬爾科夫組合模型、BP神經網絡模型、 FOA-SVM模型預計值對比分析的方法,對FOA-SVM模型的性能進行評價。
3.1 建立回歸模型
將參數值輸入SPSS軟件,設腐蝕速率y 為因變量,硫含量χ 1、酸值χ 2、溫度χ 3、流速χ 4、壓力χ 5為自變量。 FOA-SVM多元線性回歸模型采用逐步回歸的方法,針對影響因素變量對因變量的影響程度進行分析比較。建立多元性回歸模型時,為了使得回歸模型具有良好的解釋能力和預測效果,自變量的選擇準則為:
(1)自變量對因變量呈線性相關,且影響效果顯著;
(2)相關程度比較,自變量之間應低于因變量與自變量之間的的相關程度;
(3) 預測值的確定,自變量應完全滿足因變量的統計數據。
優選自變量過程中,當回歸方程中所有自變量對因變量各自影響顯著時,再考慮從其他未選中變量代人方程,循環往復直至所有自變量優選后,求解結束。由逐步回歸法得到的回歸方程為:
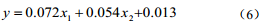
由此可以看出,逐步回歸忽略了溫度、流速兩個變量,壓力對管道的腐蝕速率影響不大。而回歸方程中硫含量和酸值的Sig值都為0,具有統計顯著性。得到的回歸方程的調整R 方為0.307,具有較好的擬合優度。
對模型所有數據進行殘差分析,優化模型。結果顯示6、 8、 9號三組數據的殘差絕對值殘差較大,忽略這三組數據,重新建立回歸方程,調整R 方為0.426,滿足要求。得到結果為:
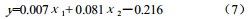
3.2 腐蝕速率預測及分析
基于FOA模型優化回歸參數C 和g ,設定群體個數為25,遺傳代數為200, C參數范圍[0,500], g參數范圍[0,100]。得到的優化參數C1和g1為0.041和0.0128輸入FOA-SVM模型訓練,結果見圖 2。圖 2中除6、 8和9三個樣本外,其他訓練后的樣本和實測值具有很好的擬合性。

3.3 FOA-SVM模型評價
為了體現FOA-SVM模型的優越性,使用某輸油管道實驗數據對FOA-SVM模型進行檢驗,將其結果與灰色馬爾科夫組合模型[4]、 BP神經網絡模型[5]兩種方法計算結果進行比較,見表 2。

從表 2中知, FOA-SVM預測模型預測結果的方差和均差分別為0.0374、 1.397×10-3,從誤差角度分析來看, FOA-SVM 模型預測值方差、均差都小于其他算法,說明FOA-SVM 模型具有相對較高的預測精度;從擬合效果來看, FOA-SVM 模型的平方相關系數高于其他模型,說明FOA-SVM 具有較好的擬合效果。
4 結論
(1)運用新建的FOA-SVM模型對天然氣場站工藝管道內腐蝕速率進行了預測該模型預計的方差為1.397×10-3,均差為0.0374,并與灰色馬爾科夫組合模型 、 BP神經網絡模型預測結果的對比分析,具有較好的泛化能力和較強的預測功能,可以相對準確、高效地對輸油管道內腐蝕速率進行預測。
(2)FOA-SVM模型算法充實了管道內腐蝕速率的預測方法,雖然能夠準確、高效預測管道內腐蝕速率,但該模型針對樣本數目多時,存在訓練消耗時間長、效率低的缺點,今后在預測效率問題上還需進一步研究。
參考文獻:
[1]陳浩力,呂仁軍,姜煒,李尚澤,等. 基于Excel的GM(1,1)模型在預測油氣管道腐蝕速率中的應用[J]. 腐蝕與防護,2014,04:378-380.
[2]劉曉東,李著信. 基于灰色組合模型的管道腐蝕速率預測[J]. 壓力容器,2007,03:15-19.
[3]王曉光,張弢,周慧. 基于LS-SVM的管道腐蝕速率灰色組合預測模型[J].數學的實踐與認識,2014,07:82-87.
[4]張宏偉,朱志潔,霍丙杰,等.基于改進的FOA-SVM導水裂隙帶高度預測研究[J].中國安全科學學報,2013,10:9-14.
[5]陳永紅,張大發,王悅民,彭桂初.基于灰色馬爾科夫組合模型的管道腐蝕速率預測方法[J].核動力工程,2009,30(02):95-98.
[6]胡松青,石鑫,胡建春,任振甲,郭愛玲,高元軍.基于BP神經網絡的輸油管道內腐蝕速率預測模型[J]. 油氣儲運,2010,29(06):448-450+398.
[7]丁世飛,齊丙娟,譚紅艷. 支持向量機理論與算法研究綜述[J]. 電子科技大學學報,2011,01:2-10.
[8]顧亞祥,丁世飛. 支持向量機研究進展[J]. 計算機科學,2011,02:14-17.
[9]張學工.關于統計學習理論與支持向量機[J].自動化學報, 2000,26(1): 32-43.
[10]Pan Wentsao. A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge-Based Systems, 2011,26(7):69-74.
[11]牛培峰,麻紅波,等. 基于支持向量機和果蠅優化算法的循環流化床鍋爐Nox排放特性研究[J]. 動力工程學報,2013,33(4):267-271.
[12]張勇,夏樹發,唐冬生. 果蠅優化算法對多峰函數求解性能的仿真研究[J]. 暨南大學學報(自然科學與醫學版),2014,01:82-87.
[13]寧劍平,王冰,李洪儒,許葆華. 遞減步長果蠅優化算法及應用[J]. 深圳大學學報(理工版),2014,04:367-373.[14]高東磊,劉友寬,蘇杰,等. 果蠅優化算法和粒子群優化算法的應用對比[J].儀器儀表用戶,2013,04:83-84+41.
作者:王志月, 1985年生,中石油管道有限責任公司西氣東輸分公司規劃計劃處, 2009年畢業于北京航空航天大學技術經濟及管理專業。現主要從事油氣管道項目后評價及計劃管理工作。
上篇:
下篇:




 甘公網安備 62010202003034號
甘公網安備 62010202003034號 
